In this post I'll show a little program written in JavaFX Script that exercises some of its features such as graphics, data binding and programming language interaction.
This is the first of a series of posts exploring these features across different platforms such as Silverlight or Flex.
The example
A little program that calculates and plots a polynomial that touches four points selected by the user. The user can move any of the given points in the screen and the polynomial will be recalculated and replotted while moving it.
Neville's algorithm
The Neville's algorithm is used to calculate the polynomial that traverses the points selected by the user.
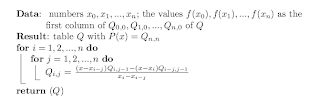
The user will select a series of points (x0,y0),(x1,y1),etc. that will be used as the input for this algorithm given that y0 = f(x0). Each entry of the Q matrix will stored as a
Polynomial object, so the final result Qn,n will be the Polynomial to be plotted.More information on this algorithm can be found in its Wikipedia page, its MathWorld page or a Numerial Analysis book such as the one by Burden & Faires.
JavaFX Script
Although JavaFX Script is a very interesting language, the biggest problem of working with it today its that is still on development, so there're many sites that contain tutorials and code snippets that references APIs or language constructs that are no longer valid. The James Weaver’s JavaFX Blog
and the JavaFX wiki were very useful resources to find out about the latest updates. Also the Converting JavaFX™ Script Programming Language Code from Interpreted to Compiled Syntax guide provides nice information on language changes.
I think this will be solved as soon a the first official release of the JavaFX SDK is published.
For now, the code snippets shown in this post were created using the build from July 11, 2008.
The program
The final program looks like this:
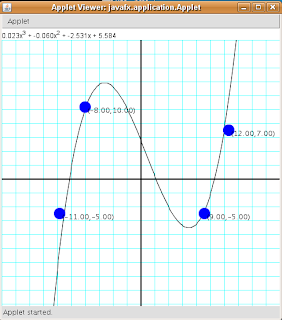
The applet can also be found here.
Implementing Neville's algorithm
In order to obtain the polynomial for the given selected points using Neville's algorithm we required a polynomial class with a couple of operations for multiplication and addition.
class Polynomial {
attribute coefficients : Number[];
function evaluate(x:Number):Number {
var result = 0.0;
for(i in [0..(sizeof coefficients) - 1]) {
result = result + coefficients[i]*Math.pow(x,i);
}
return result;
}
function multiplyByTerm(coefficient:Number,exponent:Integer):Polynomial {
var origExponent = sizeof coefficients;
if (coefficient == 0.0) {
return Polynomial{coefficients:[]}
} else {
return Polynomial {
coefficients: for (i in [0 .. (origExponent + exponent - 1) ])
if (i < exponent) 0
else coefficients[i - exponent]*coefficient
}
}
}
function multiply(p : Polynomial):Polynomial {
var parts = for (i in [0 .. (sizeof coefficients) - 1])
p.multiplyByTerm(coefficients[i],i);
var result = Polynomial{coefficients:[]};
for (part in parts) {
result = result.add(part);
}
return result;
}
function add(p : Polynomial):Polynomial {
var length1 = sizeof coefficients;
var length2 = sizeof p.coefficients;
var result:Number[];
if (length1 == length2) {
result = for(i in [0 .. length1 - 1])
coefficients[i] + p.coefficients[i];
} else {
if (length1 > length2) {
result = for(i in [0 .. length2 - 1])
coefficients[i] + p.coefficients[i];
for (i in [length2 .. length1 -1]) {
insert coefficients[i] into result
}
} else {
result = for(i in [0 .. length1 - 1])
coefficients[i] + p.coefficients[i];
for (i in [length1 .. length2 -1]) {
insert p.coefficients[i] into result
}
}
}
return Polynomial {
coefficients: result
};
}
function toString():String {
var result:java.lang.StringBuilder = new java.lang.StringBuilder();
var firstTime = true;
result.append("<html>");
for (i in [0 .. (sizeof coefficients) - 1]) {
var theIndex = (sizeof coefficients) - 1 - i;
if (Math.abs(coefficients[theIndex]) > 0.000001) {
if (not firstTime) {
result.append(" + ");
}
if (theIndex != 0) {
result.append("{%3.3f coefficients[theIndex]}x");
if (theIndex != 1) {
result.append("<sup>{theIndex}</sup>");
}
} else {
result.append("{%3.3f coefficients[theIndex]}");
}
firstTime = false;
}
}
result.append("</html>");
return result.toString();
}
}
Some elements of the JavaFX Script language that were really useful include the Sequence Comprehensions. Also the embedded expressions in string are an interesting feature.
An element to convert the coordinates between the screen and the Cartesian plane is also required to implement the algorithm.
The following code shows the implementation of this converter.
class PlaneToScreenConverter {
attribute screenMaxX : Number;
attribute screenMaxY : Number;
attribute screenMinX : Number;
attribute screenMinY : Number;
attribute planeMinX : Number;
attribute planeMinY : Number;
attribute planeMaxX : Number;
attribute planeMaxY : Number;
function convertToScreenX(x:Number):Integer {
var m = ((screenMaxX - screenMinX)/(planeMaxX - planeMinX));
var b = screenMinX - planeMinX*m ;
return (m*x + b).intValue();
}
function convertToScreenY(y:Number):Integer {
var m = ((screenMaxY - screenMinY)/(planeMaxY - planeMinY));
var b = screenMinY - planeMinY*m ;
return (m*y + b).intValue();
}
function convertToPlaneX(x:Integer):Number{
var m = ((planeMaxX - planeMinX)/(screenMaxX - screenMinX));
var b = planeMinX- screenMinX*m ;
return (m*x + b).intValue();
}
function convertToPlaneY(y:Integer):Number {
var m = ((planeMaxY - planeMinY)/(screenMaxY - screenMinY));
var b = planeMinY - screenMinY *m ;
return (m*y + b).intValue();
}
}
Finally we can implement the algorithm as follows:
class MRow {
attribute polynomials : Polynomial[];
}
class NevilleCalculator {
attribute converter : PlaneToScreenConverter;
function createPolynomial(points: FunctionPoint[]):Polynomial {
var numberOfPoints = sizeof points;
var matrix = for(i in [0..numberOfPoints - 1])
MRow {
polynomials:(for (j in [0..i])
Polynomial{coefficients:[]})} ;
for(i in [0..numberOfPoints - 1]) {
matrix[i].polynomials[0] =
Polynomial {
coefficients:[ converter.convertToPlaneY(points[i].y) ]
};
}
var xs = for(i in [0..numberOfPoints - 1]) converter.convertToPlaneX(points[i].x);
var ys = for(i in [0..numberOfPoints - 1]) converter.convertToPlaneY(points[i].y);
for(i in [1..numberOfPoints-1]) {
for(j in [1..i]) {
var q = xs[i]-xs[i-j];
var p1 = Polynomial { coefficients: [-1.0*xs[i-j]/q,1.0/q] };
var p2 = Polynomial { coefficients: [xs[i]/q,-1.0/q] };
matrix[i].polynomials[j] =
p1.multiply(matrix[i].polynomials[j-1]).add(p2.multiply(matrix[i-1].polynomials[j-1]));
}
}
return matrix[numberOfPoints-1].polynomials[numberOfPoints-1];
}
}
The
MRow class was created because I was unable to create a sequence of sequences.Plotting the function
In order to generate screen points for a given polynomial, a
FunctionPlotter class was created as follows:
class FunctionPlotter {
attribute converter : PlaneToScreenConverter;
attribute steps = 250;
attribute initialX = -1.0;
attribute finalX = 1.0;
attribute poly = Polynomial {
coefficients:[0,0,1]
}
on replace {
points = getPolyPoints();
}
attribute points = getPolyPoints();
function getPolyPoints():Number[] {
var m = (finalX - initialX)/(250 - 0);
var b = finalX - m*250;
var increment = Math.abs(converter.planeMaxX - converter.planeMinX) / steps;
var currentX = Math.min(converter.planeMaxX , converter.planeMinX);
var i = 0;
var result = for (x in [0..steps*2 - 1]) 1.0;
while (i < steps*2) {
var currentY = poly.evaluate(currentX);
result[i] = converter.convertToScreenX(currentX)*1.0;
result[i+1] = converter.convertToScreenY(currentY)*1.0;
currentX = currentX + increment;
i = i + 2;
}
return result;
}
}
Connecting all the elements
Now that we have all the pieces of the program we can connect them using data binding.
Data binding provides a very nice way for expressing connections between parts of the UI and the model of the application.
For our program we want to allow the user to move around the control points (the blue circles) and have the polynomial recalculated and replotted while moving them. In order to accomplish this we need to create the following databinding connections:
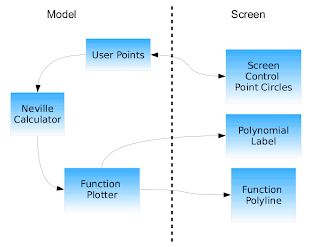
The code that represents the "model" section of the diagram is the following:
var userPoints =
Domain {
points: [
FunctionPoint{
x: 100
y: 300 },
FunctionPoint{
x: 200
y: 400 },
FunctionPoint{
x: 350
y: 300 },
FunctionPoint{
x: 400
y: 200 }
]
}
var converter = PlaneToScreenConverter {
screenMaxX: 480
screenMaxY: 0
screenMinX: 0
screenMinY: 480
planeMinX: -20
planeMinY: -20
planeMaxX: 20
planeMaxY: 20
}
var nevilleCalculator = NevilleCalculator {
converter: converter
}
var plotter = FunctionPlotter {
poly: bind nevilleCalculator.createPolynomial(
for(p in userPoints.points)
FunctionPoint{x:p.x,y:p.y})
converter: converter;
}
Notice that in the
bind expression of the poly property of the FunctionPlotter we use a for comprehension instead of passing the complete collection. This is required to allow the update of the polynomial when moving just one point.The UI part of the program looks like this:
Application {
stage:
Stage {
content:
ComponentView {
component:
BorderPanel {
background: Color.WHITE
top:
Label {
text: bind plotter.poly.toString()
}
center:
Canvas {
content: [
...
]
}
}
}
}
}
Notice that the label is also bound to the polynomial of the function plotter.
The plotted function line and the control points are located inside the canvas with the following code:
Polyline {
stroke:Color.BLACK
points: bind plotter.points
},
Group {
content: bind for (p in userPoints.points)
Group {
content: [
Circle {
centerX: p.x
centerY: p.y
radius:10
fill: Color.BLUE
var dragStartX:Number;
var dragStartY:Number;
onMousePressed:
function(event:MouseEvent) {
dragStartX = p.x;
dragStartY = p.y;
}
onMouseDragged:
function(event:MouseEvent):Void {
p.x = dragStartX + event.getDragX();
p.y = dragStartY + event.getDragY();
}
},
Text { x: p.x+4,y:p.y+10,
content: bind "({%3.2f converter.convertToPlaneX(p.x)},{%3.2f converter.convertToPlaneY(p.y)})" }
]}
}
The mouse pressed and mouse dragged handler are used to allow the user to move the control points.
Also inside the canvas is the code for the axis and the grid.
Group {
content: for(x in [0 .. Math.max(converter.screenMaxX,converter.screenMinX)/24])
Line {
stroke:Color.CYAN
startX: x*24, startY:converter.screenMinY
endX:x*24 , endY:converter.screenMaxY
}
},
Group {
content: for(y in [0 .. Math.max(converter.screenMinY,converter.screenMaxY)/24])
Line {
stroke:Color.CYAN
startX:converter.screenMinX,startY:y*24
endX:converter.screenMaxX, endY:y*24
}
},
Line {
startX: Math.abs((converter.screenMaxX - converter.screenMinX)/2)
startY: converter.screenMinY
endX: Math.abs((converter.screenMaxX - converter.screenMinX)/2)
endY: converter.screenMaxY
stroke:Color.BLACK
strokeWidth:2
},
Line {
startX: converter.screenMinX
startY: Math.abs((converter.screenMaxY - converter.screenMinY)/2)
endX: converter.screenMaxX
endY: Math.abs((converter.screenMaxY - converter.screenMinY)/2)
stroke:Color.BLACK
strokeWidth:2
},
Final words
JavaFX Script provides a nice programming language and powerful graphics and UI elements. One of the most interesting features is data binding. It will be very interesting to see how this feature is implemented in the other platforms.
The biggest problem right now is that JavaFX Script is on development so it's difficult to get documentation of the last changes. Also another problem is that right now in order to create an applet all the Jars of the distribution must be included adding a couple of MB to the size of final download.
Code for this post can be found here.
The applet can also be found here.