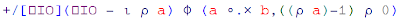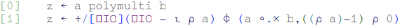Printing Scheme-like expressions using pretty printing combinators

In this post I'm going to show a small printer for Scheme-like expressions using pretty printing combinators in Haskell.

The data type definition for these expressions looks like this:

data Expr = ScSymbol String
            | ScString String
            | ScNumber Integer
            | ScDouble Double 
            | ScCons Expr Expr
            | ScNil
            | ScBool Bool
            | ScQuote Expr
     deriving Show

The pretty printing combinator library is located in the Text.PrettyPrint.HughesPJ package.

import Text.PrettyPrint.HughesPJ 

toStringP :: Expr -> Doc

The Doc data type represents a document to be printed. The definition for printing the atomic expressions looks pretty straightforward:

toStringP (ScSymbol name) = text name
toStringP (ScNumber num) = integer num
toStringP (ScDouble num) = double num
toStringP ScNil = text "()"
toStringP (ScQuote exp) = text "'" <> (toStringP exp)
toStringP (ScBool value) = text $ if value then "#t" else "#f"
toStringP (ScString str) = doubleQuotes $ text str

This code uses the text, integer and double functions to generate documents for each atomic part.

Now, the interesting part is defining the way to print ScCons which represent linked lists. The definition looks like this:

toStringP (ScCons first rest) = parens ( hang (toStringP first) 3  (sep $ toStringPCons rest))
  where
     toStringPCons (ScCons part rest) =  ((toStringP part) : (toStringPCons rest))
     toStringPCons ScNil = []
     toStringPCons other = [(text ".") , (toStringP other) ]

Here we use just three combinator functions:

1. parens: which creates a document that will be rendered inside parentheses
2. sep: which combines document parts depending on the context
3. hang: which will allow us to add a nice effect to composed expressions by nesting the contents when necessary. In this case we specify indentation by 3 characters.

The following function is used to parse the expressions using a parser from a previous post and then print the result with a given style.

    parseAndRender style text =
       case (parseIt text) of
         Right parsed -> putStr $ renderStyle style  $ toStringP parsed
         _ -> putStr "ParseError"

Now we can print an example:

    smallTest style =
      parseAndRender style "(html (head (title \"Hello world\")) (body (p \"Hi\") (ol (li \"First\") (li \"Second\"))))"

We can print using the default style like using the style definition:

*SCPPrint> smallTest style
(html
    (head (title "Hello world"))
    (body (p "Hi") (ol (li "First") (li "Second"))))

The default style definition specifies a line width of 100 characters. We can modify it to be shorter, for example:

*SCPPrint> smallTest style { lineLength =  40 }
(html
    (head
        (title "Hello world"))
    (body
        (p "Hi")
        (ol
            (li "First")
            (li "Second"))))

It is impressive what can be accomplished with such a small number of definitions. For more information about this pretty printing combinator library and its design process see: The Design of a Pretty-printing Library by John Hughes

A quick look at Haskell records

While reading the Parsec documentation I learned about a nice technique used to create language definitions. For example:

idSymbol = oneOf ":!$%&*+/<=>?@\\^|-~"

schemeLanguageDef :: LanguageDef st
schemeLanguageDef = emptyDef { 
                   commentLine = ";;"
                   , identStart = letter <|> idSymbol
                   , identLetter = alphaNum <|> idSymbol
                   , opStart = parserZero
                   , opLetter = parserZero
                 }

In this case we are creating a small language definition based on emptyDef. We're saying that we want all what emptyDef has but changing the values of commentLine, identStart, identLetter, opStart and opLetter.

The Text.Parsec.Language package contains several predefined language definitions which you can use to create yours. Some of these definitions are based on each other, for example the haskell98Def and haskellStyle. This is accomplished using Haskell record syntax for defining data types.

Records in Haskell allow the creation of abstract data type definitions that contain named fields . For example, here's a small definition of a data type to store the information of an editor color theme:

data Theme = ColorTheme {
                     keywordsColor :: Color,
                     backgroundColor :: Color,
                     fontSize :: Int,
                     operatorsColor :: Color,
                     literalsColor :: Color
                }
        deriving Show

An instance of this record can be created as follows:

   baseTheme = ColorTheme { keywordsColor = Black,
                            backgroundColor = White,
                            fontSize = 10,
                            operatorsColor = Black,
                            literalsColor = Black }

One nice feature of Haskell records is that it allows the creation of a new record instance based on a existing one. Back to our artificial example, say that we want to create a dark theme which is the same as the base but with colors inverted.

   darkTheme = baseTheme {
                           keywordsColor = White,
                           backgroundColor = Black,
                           operatorsColor = White,
                           literalsColor = White
                         } 

Here we're saying that we want a copy of baseTheme with keywordsColor, backgroundColor, operatorsColor and literalsColor changed to another value.

Pattern matching can be used to extract parts of the record. For example, say that we want to define a function to increase the current font size of a theme:

  increaseFontSize :: Int -> Theme -> Theme
  increaseFontSize amount theme@ColorTheme { fontSize = currentFontSize} =
        theme { fontSize = currentFontSize + amount } 

We can use this definition :

*Tests> increaseFontSize 5 baseTheme
ColorTheme {keywordsColor = Black, backgroundColor = White, fontSize = 15, operatorsColor = Black, literalsColor = Black}

Also accesor functions are defined for each part of the record. For example:

*Tests> backgroundColor baseTheme
White

For future posts I'm going to explore similar features that exist in other programming languages.

Creating a small parser using Parsec

In this post I'm going to show a small parser for a Scheme-like language written in Haskell using the Parsec parsing combinator library.

We're going to start by defining an AST for Scheme-like expressions:

data Expr = ScSymbol String
            | ScString String
            | ScNumber Integer
            | ScDouble Double 
            | ScCons Expr Expr
            | ScNil
            | ScBool Bool
            | ScQuote Expr
     deriving Show

For this experiment I'm going to use the Text.Parsec.Token and Text.Parsec.Language packages which have useful functions for creating language parsers.

idSymbol = oneOf ":!$%&*+/<=>?@\\^|-~"

schemeLanguageDef :: LanguageDef st
schemeLanguageDef = emptyDef { 
                   commentLine = ";;"
                   , identStart = letter <|> idSymbol
                   , identLetter = alphaNum <|> idSymbol
                   , opStart = parserZero
                   , opLetter = parserZero
                 }

schemeTokenParser = makeTokenParser schemeLanguageDef

TokenParser {
   identifier = idParser,
   reservedOp = opParser,
   stringLiteral = stringLiteralParser,
   parens = parParser,
   lexeme = lexParser,
   naturalOrFloat = naturalOrFloatParser
} = schemeTokenParser

Given these definitions we get parsers for identifiers, numbers, string literals "for free".

Boolean literals are parsed using the following parser:

boolLiteral = lexParser (
                 do 
                   char '#'
                   val <- (char 't') <|> (char 'f')
                   return $ ScBool $ val == 't'
             )

Basic quotations are parsed as follows:

quoteParser = lexParser (
              do 
                char '\''
                val <- expressionParser
                return $ ScQuote val
          )

Atomic expressions are parsed as follows:

atomParser =
   (do 
      id <- idParser
      return $ ScSymbol id)
   <|>
    (do 
       fnumber <- naturalOrFloatParser
       return $ case fnumber of
                Left num -> ScNumber num
                Right num -> ScDouble num)
   <|>        
    (do str <- stringLiteralParser
        return $ ScString str)
   <|> boolLiteral
   <|> quoteParser

Next we need to consider S-Expressions. This kind of expressions are combinations of the above elements surrounded by parentheses.

For example:

(+ 1 2 3)

dottedSuffixParser =     
   do 
      dotParser
      finalExpr <- expressionParser
      return finalExpr

parExpressionParser = 
   do (exprs, last) <- parParser 
                (do 
                   seq <- many expressionParser
                   dottedSuffix <- optionMaybe dottedSuffixParser 
                   return (case dottedSuffix of
                            Just lastExpr -> (seq, lastExpr)
                            Nothing -> (seq, ScNil)))
      return $ foldr ScCons last exprs

As shown above, the parser need to verify if there was a dot ('.') before the last element for example:

(1 . 2)

More details on the dot syntax can be found here.
Finally we define expressions:

       expressionParser =
            atomParser <|> parExpressionParser


       parseIt input = parse expressionParser "" input

We can use this function to parse this expressions as follows:

*SCParser> parseIt "(- x 1)"
Right (ScCons (ScSymbol "-") (ScCons (ScSymbol "x") (ScCons (ScNumber 1) ScNil)))

There's a great a series of articles on implementing a Scheme interpreter in Haskell called "Write Yourself a Scheme in 48 Hours/Parsing" which is a great source of information on this topic.

A call-with-current-continuation example

The call-with-current-continuation (or call/cc for short) function in Scheme allows the creation of powerful control structures. It basically allows you to capture the current state of a computation as a first class value. This value could be assigned to a variable and invoked later.

For a great introduction to this function see the call/cc entry in the Community-Scheme-Wiki .

The following toy example shows how this function is used to do an incremental search inside a tree. Say that you have the following tree structure definition:

(define tree-data
    '(html
        (head (title "test"))
        (body
           (p "foo" (i "goo"))
           (ol
            (li "xoo" (i "moo"))
            (li (i "loo")))
           (p))))

We want to define a function to search for elements identified by a predicate. For example, if looking for a "i" element we can write:

(define (is-italic? element)
  (and (list? element) 
       (not (null? element))
       (eq? 'i (car element))))

We want to create a function to perform an incremental search inside a tree structure. That is, we want to find the first element and then request the next element if needed.

Here's a demo of the function we want to create:

> (define hit (search is-italic? tree-data))
                                           
> hit
((i "goo") #<continuation>)
> (set! hit (get-next-result hit))
> hit
((i "moo") #<continuation>)
> (set! hit (get-next-result hit))
> hit
((i "loo") #<continuation>)
> (set! hit (get-next-result hit))
> hit
(() #<continuation>)

This function is defined using call-with-current-continuation as follows:

(define (search pred? tree)
  (call-with-current-continuation
   (lambda (c)
     (searching pred? tree c))))

(define (searching pred? tree return)
  (set! return
        (call-with-current-continuation
         (lambda (continuation)
           (if (pred? tree)
               (return (list tree continuation))
               return))))
  (if (list? tree)
      (for-each
       (lambda (item)
         (set! return (cadr (searching pred? item return))))
       tree))
  (list '() return))

The entry point is the search function which captures the current continuation in the return variable. This continuation value allows us to jump to the point where call-with-current-continuation was called. We pass this value to the searching function which contains the logic to search inside the tree.

The first expression of the searching function seems confusing since it contains another call to call-with-current-continuation and an assignment of return. This code is used to do the following things:

1. Return a search result (remember that return contains a continuation)
2. Capture the current state of the tree traversal (this is done by the call-with-current-continuation call)

...
  (set! return
        (call-with-current-continuation
         (lambda (continuation)
           (if (pred? tree)
               (return (list tree continuation))
               return))))
...

Notice that a search result contains two things:

1. The tree fragment that makes the predicate true
2. The continuation of the point where the element was found (which can be used to restore the traversal)

One key thing to understand is that we change the value of return to the result of the call/cc call. This is done this way because we will change the return continuation to retrieve new results. This is done using the get-next-result function as follows:

(define (get-next-result result)
  (if (not (null? (car result)))
      (call-with-current-continuation (cadr result))
      result))

Calling call-with-current-continuation with the last captured continuation will result on setting it to the return variable in searching.

A quick look at APL

In this post I'm going to show an implementation of polynomial multiplication written in APL and the steps to create it.

APL

APL is an array oriented programming language which means it's good for manipulating vectors, matrices and other kinds of arrays.

APL has many interesting characteristics among them is its syntax which uses non ASCII characters .

Here's a very nice video showing how to implement the Conway's Game Of Life in APL:



A very nice APL resource is the APL Wiki it has lots of information. Another very nice resource is The FinnAPL Idiom Library which contains lots little examples of code. Another nice resource is Vector the journal of the British APL Association which has information on the community around APL related languages.

The examples presented in this post were written using NARS2000 a nice open source implementation of APL.

Polynomial multiplication

As with a previous post on J I'm going to show the implementation of polynomial multiplication .

The following example shows the process of multiplying two polynomials:

(4x3 - 23x2 + x + 1) * (2x2 - x - 3)

= ((4x3 - 23x2 + x + 1) * 2x2) +
((4x3 - 23x2 + x + 1) * -x) +
((4x3 - 23x2 + x + 1) * -3)

= (8x5 - 46x4 + 2x3 + 2x2) +
(-4x4 + 23x3 - x2 - x) +
(-12x3 + 69x2 - 3x - 3)

= (8x5 - 50x4 + 13x3 + 70x2 - 4x - 3)

This example will be used to illustrate the parts of the code in the following sections.

The program

The final program to calculate polynomial multiplication looks like this:



Where a and b are the polynomials.

As with the previous post on J I'm sure there's a shorter way to write this program
(the number of parenthesis seems to indicate this!).

One key aspect to understand APL code is to remember that it evaluates expressions from right to left. See the Order of execution section of the APL Wiki for more information.

A description of each part of this program is presented in the following sections.

Polynomial representation

To represent polynomials we're going to use vectors the following way:

For:

(4x3 + 23x2 + x + 1)

the array will be:

1 1 23 4

In APL arrays are written as sequences of numbers separated by spaces (as above). You can manipulate this values easily, for example here we create two variables with two polynomials and add them:



In order to multiply each element of the array by a value we can simply write:

Outer product

The outer product operator lets you apply an operation to all the combinations of the elements of the operands. For example if we want to multiply each value of the two arrays representing the polynomials we want to multiply we can write:

Creating a matrix of intermediate polynomials

We need to obtain a matrix with the intermediate polynomials given the result of the outer product. But first I'm going to introduce the rho function. This function can be used to with one argument (monadic) to obtain the dimensions of the given array for example:



Or it can be used with two arguments (dyadic) to create an array of the given shape.



We can use this function combined with comma function to expand the matrix of polynomials:




The iota function lets you, among other things, create arrays of sequences of values. We're going to use it to create the values used to rotate each polynomial in our matrix:



The rotation of each matrix element is performed using the rotate function as follows:





The final step is to sum every vector in this matrix. We can do that by using the reduce operator (/) . This operator lets you apply a dyad operation to every element of an array accumulating the result. For example:




The nice thing about it is that if you apply it to a matrix, it will do the right thing by summing up every 1d vector. In our case we need to sum the rows so we change the axis of the operation.

Index origin

Before defining the final function we need to take an additional consideration. There is a system variable which modifies the origin of the iota function among other things. For example:



In other to make our code independent of the value of IO by using it instead of references to '1' as above.

Defining a function

The final function definition looks like this:




We can use this function as follows:

IronPython & WPF: Data binding with TreeView's selected element

In this post I'm going to show a small example of using data binding with the selected element of a WPF TreeView with an IronPython class.

A couple of days ago I had the necessity of using data binding to keep track of the selected value of a WPF TreeView . At first it seemed to be an easy task so I wrote:

<TreeView SelectedValue="{Binding selected, Mode=TwoWay}" ... />

Running this code results on the following error:

SystemError: 'Provide value on 'System.Windows.Data.Binding' threw an exception.' Line number '12' and line position '7'.

The problem is that the SelectedValue (and SelectedItem) property is read-only.

There are several ways to deal with this problem. One alternative is to use a technique similar to the one described in the "Forwarding the Result of WPF Validation in MVVM" post. We're going to define an attached property which works as an "output only" property that could be used with data binding.

Attached property definition

I couldn't find a way to wrote the definition of the attached property in IronPython because it needed to be instanciated by XamlReader. So the definition was written using C#:

using System.Windows.Markup;
using System.Windows;
using System.Windows.Controls;
using System.IO;
using System.Collections.ObjectModel;


namespace Langexplr 
{
   public static class TreeViewSelectedBehavior
   {
      public static readonly DependencyProperty MySelectedProperty = 
             System.Windows.DependencyProperty.RegisterAttached(
                                       "MySelected",
                                       typeof(object),
                                       typeof(TreeViewSelectedBehavior)
                                    );
      public static object GetMySelected(TreeView t)
      {
         return t.GetValue(MySelectedProperty);
      }

      public static void SetMySelected(TreeView t, object theValue)
      {
         t.SetValue(MySelectedProperty, theValue);
      }

                                    
      public static readonly DependencyProperty SelectedHelperProperty =
             System.Windows.DependencyProperty.RegisterAttached(
                                       "SelectedHelper",
                                       typeof(TreeViewSelectedHelper),
                                       typeof(TreeViewSelectedBehavior),
                                       new UIPropertyMetadata(null,OnSelectedHelperChanged)
                                    );

      public static  TreeViewSelectedHelper GetSelectedHelper(TreeView t) 
      {
          return (TreeViewSelectedHelper)t.GetValue(SelectedHelperProperty);
      }

      public static void SetSelectedHelper(TreeView t, 
                                           TreeViewSelectedHelper theValue) 
      {
          t.SetValue(SelectedHelperProperty, theValue);
      }
      static void OnSelectedHelperChanged(
                    DependencyObject depObj, 
                    DependencyPropertyChangedEventArgs e)
      {
         ((TreeViewSelectedHelper)e.NewValue).Register((TreeView)depObj);
      }

   }

This class define two properties:

• MySelected: the output property that is used to set the selected element in the view model
• SelectedHelper: which is used to as an object that modifies the value of MySelected when the selected item changes(see below).

The following helper class is used to subscribe the SelectedItemChanged event and change "MySelected" .

public class TreeViewSelectedHelper 
   {
       public TreeViewSelectedHelper() { }
       void SelectedItemChanged(object sender, 
                                RoutedPropertyChangedEventArgs<object> args)
       {
           (sender as TreeView).SetValue(
                        TreeViewSelectedBehavior.MySelectedProperty,
                        ((sender as TreeView)).SelectedItem);
       }
       public void Register(TreeView t)
       {
           t.SelectedItemChanged += SelectedItemChanged;
       }
   }

}

We can now compile this class:

set NETFX4=c:\WINDOWS\Microsoft.NET\Framework\v4.0.30319\
set WPFPATH=%NETFX4%\WPF
csc /debug /r:%NETFX4%System.Xaml.dll /r:%WPFPATH%\WindowsBase.dll /r:%WPFPATH%\PresentationCore.dll /r:%WPFPATH%\PresentationFramework.dll  /target:library utils.cs

The example

Having defined this attached property and helper class we can now write the following example.

<Window xmlns="http://schemas.microsoft.com/winfx/2006/xaml/presentation"
        xmlns:x="http://schemas.microsoft.com/winfx/2006/xaml"
        xmlns:utils="clr-namespace:Langexplr;assembly=utils"
        Title="TreeView selection test" Width="300" Height="300">
   <Window.Resources>
     <utils:TreeViewSelectedHelper x:Key="selHelper" />
   </Window.Resources>
   <StackPanel>

      <TextBlock Text="{Binding selected.label}"/> 
         <TreeView ItemsSource="{Binding roots}"      
                   utils:TreeViewSelectedBehavior.SelectedHelper="{StaticResource selHelper}">
             <utils:TreeViewSelectedBehavior.MySelected>
               <Binding Path="selected" Mode="OneWayToSource"/> 
             </utils:TreeViewSelectedBehavior.MySelected> 
              <TreeView.ItemTemplate>
                  <HierarchicalDataTemplate ItemsSource="{Binding children}">
       <TextBlock Text="{Binding label}"/>
    </HierarchicalDataTemplate>
       </TreeView.ItemTemplate>
         </TreeView>
   </StackPanel>
</Window>

With this XAML definition we can write the following IronPython code:

import clr
clr.AddReference("PresentationCore")  
clr.AddReference("PresentationFramework")  
clr.AddReference("WindowsBase")  
clr.AddReference('GalaSoft.MvvmLight.WPF4.dll')


from System.Windows.Markup import XamlReader
from System.Windows import Application
from System.IO import File
from System.Windows.Controls import TreeView
import System
import clrtype
from GalaSoft.MvvmLight import ViewModelBase
from System.Collections.ObjectModel import ObservableCollection


class TestModel(ViewModelBase):
   __metaclass__ = clrtype.ClrClass
   def __init__(self):
       self.name = 'algo'
       self.root = NodeModel('x1',[NodeModel('y2',[NodeModel('z2',[])]),
                                   NodeModel('y3',[])])

       self.sselected = NodeModel('',[])

   @property
   @clrtype.accepts()
   @clrtype.returns(System.Object)
   def selected(self): 
      result = self.sselected
      return result

   @selected.setter
   @clrtype.accepts(System.Object)
   @clrtype.returns()
   def selected(self, value):
      self.sselected = value
      self.RaisePropertyChanged('selected')

   @property
   @clrtype.accepts()
   @clrtype.returns(System.Object)
   def roots(self): 
      return [self.root]

   @property
   @clrtype.accepts()
   @clrtype.returns(System.String)
   def label(self): 
      return self.name
 
   @label.setter
   @clrtype.accepts(System.String)
   @clrtype.returns()
   def label(self, value):
      self.name = value
      self.RaisePropertyChanged('label')



class NodeModel:
   __metaclass__ = clrtype.ClrClass

   def __init__(self,label, initchildren):
      self.children_collection = ObservableCollection[System.Object](initchildren)
      self.name = label


   @property
   @clrtype.accepts()
   @clrtype.returns(System.Object)
   def label(self): 
      return self.name

   @property
   @clrtype.accepts()
   @clrtype.returns(System.Object)
   def children(self): 
      return self.children_collection
 

xamlFile = File.OpenRead('test.xaml')
window = XamlReader.Load(xamlFile)
window.DataContext = TestModel()
xamlFile.Close()

Application().Run(window)

By running this example we can see how the label of the selected element of the TreeView is reflected in the TextBlock defined above.

IronPython & Silverlight Part VI: Using the TreeView control

In this post I'm going to show a small example of using the Silverlight 4 TreeView control with IronPython.

Referencing System.Windows.Controls.dll

Before we start using the TreeView control we need to add a reference to System.Windows.Controls.dll . This assembly can be found in the "Microsoft Silverlight 4 Tools for Visual Studio 2010" package.

You need to copy this assembly to the location of chiron.exe (ex. IronPython2.7\Silverlight\bin) and add a reference to it in the AppManifest.xaml file.

<Deployment xmlns="http://schemas.microsoft.com/client/2007/deployment" 
            xmlns:x="http://schemas.microsoft.com/winfx/2006/xaml" 
            RuntimeVersion="4.0.50917.0" 
            EntryPointAssembly="Microsoft.Scripting.Silverlight"  
            EntryPointType="Microsoft.Scripting.Silverlight.DynamicApplication" 
            ExternalCallersFromCrossDomain="ScriptableOnly">
  <!-- Add assembly references here -->
  <Deployment.Parts>
... 
    <AssemblyPart Source="System.Windows.Controls.dll" />
  </Deployment.Parts>
...
</Deployment>

Since we're using Silverlight 4 we need to change the runtime version to "4.0.50917.0" (see this post for more details).

Using the TreeView in XAML

Now that we have access to the assembly we can use it in app.xaml.

<UserControl x:Class="System.Windows.Controls.UserControl"
 xmlns="http://schemas.microsoft.com/client/2007"
 xmlns:x="http://schemas.microsoft.com/winfx/2006/xaml"
        xmlns:sdk="clr-namespace:System.Windows.Controls;assembly=System.Windows.Controls"
        xmlns:wsdk="clr-namespace:System.Windows;assembly=System.Windows.Controls">
  <StackPanel x:Name="layout_root" Background="White">
    <TextBlock x:Name="Message" FontSize="30" Text="TreeView experiment" />
    <sdk:TreeView x:Name="tree">
       <sdk:TreeView.ItemTemplate>
           <wsdk:HierarchicalDataTemplate ItemsSource="{Binding nodes}">
               <TextBlock Foreground="Red" Text="{Binding label}" />
           </wsdk:HierarchicalDataTemplate>
       </sdk:TreeView.ItemTemplate>
    </sdk:TreeView>
  </StackPanel>
</UserControl>

TreeView data binding

The XAML file above shows that we're binding the content of the tree view to the nodes property of the data source object. Here's the definition of the Python class used for this example:

from System.Windows import Application
from System.Windows.Controls import UserControl
from System import Object
from System.Collections.ObjectModel import ObservableCollection
import clrtype
import clr

clr.AddReferenceToFile('GalaSoft.MvvmLight.SL4.dll')

from GalaSoft.MvvmLight.Command import RelayCommand


class Node:
  __metaclass__ = clrtype.ClrClass
  __clrnamespace = "LangexplrExperiments"


  def __init__(self,label,children):
    self.text = label
    self.children = children

  @property 
  @clrtype.accepts()
  @clrtype.returns(str)
  def label(self): 
     return self.text

  @property 
  @clrtype.accepts()
  @clrtype.returns(Object)
  def nodes(self): 
     return self.children



class App:
  def __init__(self):
    root = Application.Current.LoadRootVisual(UserControl(), "app.xaml")
    root.tree.ItemsSource = [Node('level1',
                                 [Node('level11',[]),
                                  Node('level12',[Node('level121',[])])
                                 ])]


App()

With this changes we can run chiron.exe /b and we get: