Using Groovy Builders to create Java3D scenes

While listening to Java Posse episode 101 I found out about a nice feature of the Groovy language called Builders.

Groovy Builders provide a unified syntax for tree-like structures. The following example shows the use of the MarkupBuilder to create an XML document.

import groovy.xml.*;

writer = new StringWriter()
builder = new MarkupBuilder(writer)

builder.document(name:"a document") {
  chapter(name:"First one") {
     page1("first page")
     page2("second page")
  }
  chapter(name:"First two") {
     page1("page 1")
    
    page2("page 2" )
    
  }
}

println(writer.toString())

This program generates the following output:

<document name='a document'>
 <chapter name='First one'>
   <page1>first page</page1>
   <page2>second page</page2>
 </chapter>
 <chapter name='First two'>
   <page1>page 1</page1>
   <page2>page 2</page2>
 </chapter>
</document>

The nice thing about Groovy builders is that can also be used to create other kinds of tree structures such as Swing GUIs(SwingBuilder) or Ant tasks(AntBuilder) among others. For example, using the Swing builder you can create a simple form:

import java.awt.*
import javax.swing.*
import groovy.swing.SwingBuilder


sb = new SwingBuilder()

aFrame = sb.frame(title:"Hello World",size:[200,200]){
    panel(layout: new FlowLayout()) {
      scrollPane(preferredSize:[200,130]) {
        tree()
      }
      panel(layout:new GridLayout(1,2,15,15)){
         button(text:"Ok")
         button(text:"Cancel")
      }
    }
}
aFrame.show()

Will generate:




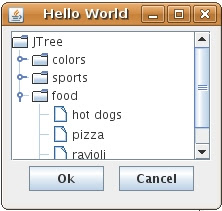
All this is possible because Groovy provides an extensible factory mechanism for this syntax. I think this makes Groovy builders a much better feature than having a just XML literals (like in VB9) because it gives the developer freedom to select other data formats (objects, JSON,binary files, S-Expressions!,etc).

In other to create a new builder you have to inherit from groovy.util.BuilderSupport and implement the following methods:

protected abstract void setParent(Object parent, Object child);
protected abstract Object createNode(Object name);
protected abstract Object createNode(Object name, Object value);
protected abstract Object createNode(Object name, Map attributes);
protected abstract Object createNode(Object name, Map attributes, Object value);

The createNode methods are used to create one node of the tree with the given name,attributes and value. The setParent method is used to connect parent and child nodes.

In this post I'm going to create the first approach of a new builder for Groovy that can be used to build Java3D scenes.

Java3D scenes are represented as a scene graph. The objects in the scene graph can be arranged in a tree structure (although references between sibling nodes can exists, hence the name). For example:



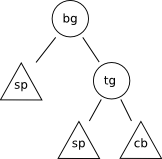
This tree represents a scene with tree objects two spheres (sp) and one cube (cb) and one transformation group (tg) and a branch group (bg). Transformation groups, as the name says, applies a transformation (rotate,scale,etc) to all of its child elements. Java3D is a huge topic which is not intended to be covered in this post, for more information check here and here.


In this post I'll only cover a couple of Java3D classes, in future posts in I'm going to try to add more elements to the Groovy builder.

The main strategy is to create a new builder class (Java3dBuidler) which creates Java3D nodes by using helpers that map attributes to Node properties and constructor arguments. This mapping is done using helpers for each node. All the code for the builder support will be created using Java although Groovy could also be used.

First of all we create the Java3dBuilder class:

public class Java3dBuilder extends BuilderSupport {
  
   HashMap<String,J3dNodeHelper> objects;
  
   public Java3dBuilder() {
       objects = new HashMap();
          
       objects.put("branchGroup",new BranchGroupHelper());
       objects.put("transformGroup",new TransformGroupHelper());
       objects.put("colorCube",new ColorCubeHelper());
       objects.put("rotationInterpolator",new RotatorInterpolatorHelper());       
   }
   ...

The Java3dBuilder constructor creates a map between the names of the elements to be used in the scene and the node creation helpers.

The J3dNodeHelper is the base class of the node creation helpers which are used to create instances of individual kinds of Java3D nodes. For example BranchGroupHelper will be used to create BranchGroup instances using the "branchGroup" name.

The setParent method as described above, creates a link between parent and child. In this case a parent must be a Java3D Group and the child a Java3D Node.

protected void setParent(Object parent, Object child) {       
  if (parent instanceof Group ) {
      Group gParent = (Group)parent;
      Node nChild = (Node)child;
      gParent.addChild(nChild);
  }
}

The createNode methods use the required node helper to create the required node .

protected SceneGraphObject createObject(String name) {
    J3dNodeHelper c = objects.get(name);
    return  (SceneGraphObject)c.create(new HashMap());       
}
protected SceneGraphObject createObject(String name,Map attributes) {
    J3dNodeHelper c = objects.get(name);
    return  (SceneGraphObject)c.create(attributes);       
}

protected Object createNode(Object name, Map atts, Object value) {
    SceneGraphObject result = null;
    String sName = (String)name;             
    SceneGraphObject current = (SceneGraphObject)getCurrent();       
    result = createObject(sName,atts);
    return result;
}

protected Object createNode(Object object, Map atts) {
    SceneGraphObject result = null;
    String sName = (String)object;
    return createObject(sName,atts);
}

protected Object createNode(Object name, Object value) {
    SceneGraphObject result = null;
    SceneGraphObject current = (SceneGraphObject)getCurrent();
    String sName = (String)name;
    result = createObject(sName);
    return result;
}

protected Object createNode(Object name) {
    SceneGraphObject result = null;
    SceneGraphObject current = (SceneGraphObject)getCurrent();
    String sName = (String)name;
    result = createObject(sName);
    return result;
}

The J3dNodeHelper class is implemented as:

public abstract class J3dNodeHelper {      
  public J3dNodeHelper() {
  }
 
  abstract protected Node createNode();
 
  protected void applyAttributes(Node aNode,Map attributes) {
  }
 
  public Node create(Map attributes) {
     Node result = createNode();
     applyAttributes(result,attributes);
     return result;
  }
}

An example of a J3dNodeHelper used for TransformGroup is the following:

public class TransformGroupHelper extends J3dNodeHelper{
 protected void applyAttributes(Node aNode,Map attributes) {                   
     TransformGroup tg = (TransformGroup)aNode;
     Set<Map.Entry<Object,Object>> s = attributes.entrySet();
     for (Map.Entry<Object,Object> e : s) {
         if (e.getKey().toString().equals("capability") &&
             e.getValue() instanceof Integer) {               
             tg.setCapability(((Integer)e.getValue()).intValue());
         } else
         if (e.getKey().toString().equals("transform") &&
             e.getValue() instanceof Transform3D) {
             tg.setTransform(((Transform3D)e.getValue()));
         }else {
             System.out.println("Could not set property "+e.getKey()+
                     " ,"+e.getValue()+","+e.getValue().getClass());
         }
     }
 }
 protected Node createNode() {
     return new TransformGroup();
 }          
}

The TransformGroupHelper class maps two TransformGroup attributes: capability and transform.

Also there're some cases where attributes have to be mapped to constructor arguments, because of properties that cannot be changed after object creation. In the case the create method must extract this values before creating the actual node . For example the helper for ColorCube class looks like this:

public class ColorCubeHelper extends J3dNodeHelper {
  protected Node createNode() {
      return new ColorCube();
  }
  protected Node createNode(double scale) {
      return new ColorCube(scale);
  }
  
  public Node create(Map attributes) {
      Node retValue;        
      if (attributes.get("scale") != null) {
          retValue = 
                createNode(
                    ((BigDecimal)attributes.get("scale")).doubleValue());
      } else {
          retValue = createNode();
      }        
      applyAttributes(retValue,attributes);
      return retValue;
  }
  
}

Now that we have all the infrastructure ready, we can start using our builder. The following example show the creation of the scene graph using our builder:

public BranchGroup createSceneGraph() {
  Java3dBuilder j3b = new Java3dBuilder()
  BranchGroup objRoot ;
  objRoot = 
    j3b.branchGroup() {
       transformGroup(
           transform:new Transform3D(
                          new Quat4f(
                                3.4f,
                                4.0f,
                                1.5f,
                                1.0f),
                          new Vector3d(),
                          1.0)) {
           colorCube(scale:0.5)
        }
  };
  objRoot.compile();
  return objRoot;
}

Which generates the scene:



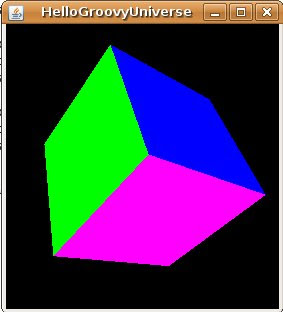
The code for scene creation of the HelloUniverse.java, included with Java3D, looks like this (removing the comments):

public BranchGroup createSceneGraph() {
  BranchGroup objRoot = new BranchGroup();

  TransformGroup objTrans = new TransformGroup();
  objTrans.setCapability(TransformGroup.ALLOW_TRANSFORM_WRITE);
  objRoot.addChild(objTrans);

  objTrans.addChild(new ColorCube(0.4));

  Transform3D yAxis = new Transform3D();
  Alpha rotationAlpha = new Alpha(-1, 4000);

  RotationInterpolator rotator =
      new RotationInterpolator(rotationAlpha, objTrans, yAxis,
             0.0f, (float) (Math.PI*2.0f));
  BoundingSphere bounds =
      new BoundingSphere(new Point3d(0.0,0.0,0.0), 100.0);
  rotator.setSchedulingBounds(bounds);
  objRoot.addChild(rotator);

    objRoot.compile();

  return objRoot;
}

If we want to create this scene using our builder we write:

public BranchGroup createSceneGraph() {
  TransformGroup tg;
  Java3dBuilder j3b = new Java3dBuilder()
  BranchGroup objRoot ;

  objRoot  = 
   j3b.branchGroup() {
     tg = transformGroup(
             capability:TransformGroup.ALLOW_TRANSFORM_WRITE) {
               colorCube(scale:0.4)
          };
     rotationInterpolator(
           alpha:new Alpha(-1,4000), 
           target:tg,
           axisOfTransform:new Transform3D(),
           minAngle:0.0,
           maxAngle:Math.PI*2.0,
           schedulingBounds:new BoundingSphere(
                   new Point3d(0.0,0.0,0.0), 100.0)
          ); 
  }

  objRoot.compile();
 return objRoot;
}

More complex scenes can be created, for example:

public BranchGroup createSceneGraph() {
  TransformGroup tg;
  Java3dBuilder j3b = new Java3dBuilder()

  BranchGroup objRoot;
  objRoot = 
    j3b.branchGroup() {
        tg = transformGroup(
               capability:TransformGroup.ALLOW_TRANSFORM_WRITE) {
               colorCube(scale:0.1)
               transformGroup(transform:new Transform3D(
                                new Quat4f(),
                                new Vector3d(0.0f,0.5f,0.5f),
                                1.0)) {
                   colorCube(scale:0.1)
               }
               transformGroup(transform:new Transform3D(
                                new Quat4f(),
                                new Vector3d(0.0f,-0.5f,0.5f),
                                1.0)) {
                   colorCube(scale:0.1)
               }
               transformGroup(transform:new Transform3D(
                                new Quat4f(),
                                new Vector3d(0.5f,0.0f,0.5f),
                                1.0)) {
                   colorCube(scale:0.1)
               }
               transformGroup(transform:new Transform3D(
                                new Quat4f(),
                                new Vector3d(-0.5f,0.0f,0.5f),
                                1.0)) {
                   colorCube(scale:0.1)
               }
    };
    rotationInterpolator(
                 alpha:new Alpha(-1,4000), 
                 target:tg,
                 axisOfTransform:new Transform3D(),
                 minAngle:0.0,
                 maxAngle:Math.PI*2.0,
                 schedulingBounds:new BoundingSphere(
                       new Point3d(0.0,0.0,0.0), 100.0)
                 ); 
  }

  objRoot.compile();
  return objRoot;
}

Will generate:



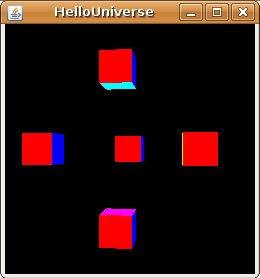
In future posts I'm going to elaborate more on this topic. In this post only four Java3D Node classes were used, more helpers need to be created in order to support Materials, Lights, Primitives,etc.

Also in the future it'll be very interesting to see what F3 is doing for Swing/Java2D and soon for 3D graphics.

List comprehensions across languages

According to Wikipedia a list comprehension is a language construct that lets you specify the contents of a list based on the set builder notation which used in mathematics to describe the members of a set.

For example in order to describe "the set of all natural numbers greater than 4 and lower than 10" using this notation we say:



A list comprehension expression is composed of the following elements:



Where:

• set member describes each element of the set. .
  
• generator generate values to be included in the set. More than one generator can be used. In the case, all possible combinations are tested.
  
• filter expressions filter generated values.

In this post I'm going to show examples written in several languages that have a construct similar to list comprehensions. Three examples are used:

1. Get all even numbers from a list

A simple example that filters the contents of a list of integers to get all the even numbers.

2. Get all the files that are greater than some given size

An example to show how list comprehensions can be used to work on elements other than numbers.

3. Solve the 4(ABCD) = DCBA puzzle

An example to show the use of several generators. This puzzle consists in finding the values of digits A,B,C,D given that ABCD*4 = DCBA where ABCD and DCBA are 4-digit numbers.


And now the code...


Haskell

The syntax of list comprehensions in Haskell can be considered syntactic sugar for the List Monad.

Syntax is described here.

Example 1:

getEvenNumbers aList  =
   [ x | x >- aList, x `mod` 2 = 0]

Example 2:

import Directory
import Monad
import IO

...

getFilesGreaterThan size directory =
  do
    contents <- getDirectoryContents directory
    files <- filterM doesFileExist $ map ((++) directory) contents
    filesWithSize <- mapM fsize files
    return [fname | (fname,fsize) <- filesWithSize, fsize >= size]
 where
   fsize f =
      do {fd   <- openFile f ReadMode;
          size <- hFileSize fd;
          hClose fd;
          return (f,size)}

Example 3:

solveABCDProblem =
  [ (a,b,c,d) |
    a <-[0..9],
    b <-[0..9],
    c <-[0..9],
    d <-[0..9],
    a /= 0,
    (1000*a + 100*b + 10*c + d)*4 ==
    (1000*d + 100*c + 10*b + a)]

F#

F# sequence comprehensions syntax is described here . One nice feature of F# sequence comprehensions is that not only lists can be used in generators, but any object implementing IEnumerable . Also the result of a sequence comprehension an IEnumerable.

Example 1:

let GetEvenNumbers (l) =
    { for i in l
      when i % 2 = 0 -> i }

Example 2:

let GetFilesGreaterThan( size ,directory) =
   let dInfo = (new System.IO.DirectoryInfo(directory))
       in { for f in dInfo.GetFiles()
            when (f.Length >= size) -> f }

Example 3:

let SolveProblem() =
   { for a in 0 .. 9
     for b in 0 .. 9
     for c in 0 .. 9
     for d in 0 .. 9
     when (1000*a + 100*b + 10*c + d)*4 =
          (1000*d + 100*c + 10*b + a) -> (a,b,c,d) }

Scala

Scala has the concept of sequence comprehensions which works with several kinds of collections.

Example 1:

def getEvenNumbers(l : List[int]) =
    for { val i <- l      
          i % 2 == 0 }         
        yield i 

Example 2:

def getFilesGreaterThan(size : int, folder : String) = {
    val folderD = new java.io.File(folder)
    for{ val f <- folderD.listFiles()      
         f.isFile()                   
         f.length() >= size
      } yield f.getName()
}

Example 3:

 def solveProblem() =
      for {
        val a <- List.range(0,9)
        val b <- List.range(0,9)
        val c <- List.range(0,9)
        val d <- List.range(0,9)
        a != 0
        (a*1000 + b*100 + c*10 + d)*4 == (d*1000 + c*100 + b*10 + a)
      } yield List(a,b,c,d)

Erlang

Erlang's list comprehensions are described here .


Example 1:

get_even_numbers(L) -> [X || X <- L, (X rem 2) == 0]. 

Example 2:

get_files_greater_than(Size,Directory) -> 
  [Fn || Fn <- filelib:wildcard(lists:append(Directory,"*")), 
         not filelib:is_dir(Fn),  
         filelib:file_size(Fn) > Size]. 

Example 3:

solve_problem() ->
   [{A,B,C,D} ||
     A <- [0,1,2,3,4,5,6,7,8,9],
     B <- [0,1,2,3,4,5,6,7,8,9],
     C <- [0,1,2,3,4,5,6,7,8,9],
     D <- [0,1,2,3,4,5,6,7,8,9],
     A /= 0,
     (1000*A + 100*B + 10*C + D)*4 == (1000*D + 100*C + 10*B + A) ].

Python

Python list comprehension syntax is described here.

Example 1:

def getEvenNumbers(l):
   return [x for x in l if x % 2 == 0]

Example 2:

def listFilesGreaterThan(size,directory):
    return [fileName
            for fileName in os.listdir(directory)
            if os.path.isfile(os.path.join(directory,fileName))
            if os.path.getsize(os.path.join(directory,fileName)) > size]

Example 3:

def solveProblem():
return [ (a,b,c,d)
          for a in range(0,9)
          for b in range(0,9)
          for c in range(0,9)
          for d in range(0,9)
          if a != 0
          if ((a*1000 + b*100 + c*10 + d)*4) ==
             (d*1000 + c*100 + b*10 + a)]

Nemerle

Nemerle list comprehensions are described here.

Example 1:

public GetEvenNumbers(l : list[int]) : list[int] {
     $[x | x in l, x % 2 == 0]
}

Example 2:

 public GetFilesGreaterThan(size : int, directory: string) : list[string] {
     def dInfo = DirectoryInfo(directory);
     $[f.Name | f in dInfo.GetFiles(),  f.Length >= size]
 }

Example 3:

 public SolveProblem() : list[int*int*int*int]{
   $[(a,b,c,d) |
     a in [0..9],
     b in [0..9],
     c in [0..9],
     d in [0..9],
     a != 0,
     (1000*a + 100*b + 10*c + d)*4 == (1000*d + 100*c + 10*b + a) ]   
 }

Boo

Because of its influence in the language, list generators in Boo are very similar to list comprehensions in Python.

Example 1:

def getEvenNumbers(l):
   return [x for x as int in l if x % 2 == 0]

Example 2:

def getFilesGreaterThan(size  as int,directory as string):
   dInfo = DirectoryInfo(directory)
   return [f.Name for f in dInfo.GetFiles() if f.Length > size]

Example 3:

def solveProblem():
    return [(a,b,c,d) 
     for a in range(0,9)
     for b in range(0,9)
     for c in range(0,9)
     for d in range(0,9)
     if a != 0 and ((1000*a + 100*b + 10*c + d)*4) == (1000*d + 100*c + 10*b + a)]

Visual Basic 9 (LINQ)

The LINQ feature of VB 9 allows the creation of expressions similar to list comprehesions. A nice feature of LINQ is that it operates with any object that implements IEnumerable<T> and also returns an IEnumerable<T> .

Example 1:

Public Shared Function  GetEvenNumbers(ByVal l as List(Of Integer)) as List(Of Integer) 
    Return New List(Of Integer) ( _
            From x in l _
            Where (x Mod 2) = 0 _
            Select x )
End Function

Example 2:

Public Shared Function GetFilesGreaterThan(ByVal size As Integer,directory As String) As List(Of FileInfo) 
     Dim dirInfo = new DirectoryInfo(directory)

     return  new List(Of FileInfo) (From f in dirInfo.GetFiles() _
             Where f.Length >= size _
             Select f)
End Function:

Example 3:

Public Shared Sub SolveProblem()
     Dim results = _
          From a in Range(0,9), _
               b in Range(0,9), _
               c in Range(0,9), _
               d in Range(0,9) _
          Where (1000*a + 100*b + 10*c + d)*4 = _
                (1000*d + 100*c + 10*b + a) AndAlso _
                a <> 0 _
          Select New {  A := a,B := b,C := c,D := d  }
     For Each result in results
        Console.WriteLine("A={0} B={1} C={2} D={3}",result.A,result.B,result.C,result.D)
     Next

End Sub


Public Shared Function Range(i as Integer,n as Integer) as List(Of Integer)
    Dim result as new List(Of Integer)()
    For i = i To n 
       result.Add(i)
    Next
    Return result
End Function

C# 3.0 (LINQ)

As with VB, the LINQ feature of C# 3.0 allows the creation of expressions similar to list comprehesions.

Example 1:

static List<int> GetEvenNumbers(List<int> l) 
{
    return new List<int>( from x in l
            where x % 2 == 0
            select x);
}

Example 2:

static List<FileInfo> GetFilesGreaterThan(int size,string directory)
{
  DirectoryInfo dirInfo = new DirectoryInfo(directory);

  return new List (
       from f in dirInfo.GetFiles()
         where f.Length >= size
         select f
  );
}

Example 3:

static void SolveProblem()
 {
    var results = 
       from a in range(0,9)
       from b in range(0,9)
       from c in range(0,9)
       from d in range(0,9)
       where (1000*a + 100*b + 10*c + d)*4 == 
             (1000*d + 100*c + 10*b + a) &&
             a != 0
       select new {
           A=a,B=b,C=c,D=d
       };


     foreach(var result in results) {
           Console.WriteLine("A={0} B={1} C={2} D={3}",
                      result.A,result.B,result.C,result.D);
     }
}

static IEnumerable<int> range(int s,int n)
{
   for(int i = s ;i <= n;i++) {
      yield return i;
   }
}

Powershell

Although not explicitly having a list comprehension feature, it's interesting to use Powershell pipeline to get a similar funcionality.

Example 1:

Function GetEvenNumbers($l) {
   $l | ?  {$_ % 2 -eq 0} 
}

Example 2:

function GetFilesGreaterThan($size, $folder) {
   get-childitem $folder | ? { $_.Length -gt $size}
}

Example 3:

Function SolveProblem() {
   (0..9) | % { $a=$_ ;(0..9) |
      % {$b = $_ ; (0..9) |
          % {$c = $_ ; (0..9) |
              % {$d = $_ ; @{a=$a;b=$b;c=$c;d=$d}} } } } | 
                ? {  ((1000*$_.a + 100*$_.b + 10*$_.c + $_.d )*4) -eq  
                      (1000*$_.d + 100*$_.c + 10*$_.b + $_.a )} | 
                  % { write-host $_.a $_.b $_.c $_.d} 
}

Others

Some other languages with list comprehensions where not covered by this post. Among this languages is Fortress(waiting for reference implementation to support this) and Perl 6 . Future posts will cover this languages.

Hello World!!!

Hello World!!!,


main = putStrLn(“Hello world!!!”)

...

class Hello {
public static void main(String[] a) {
System.out.println(“Hello World!!!”);
}
}

...

:- writeln('Hello, world!').

...

I was thinking that the best way to start this blog was to show several Hello World versions for several programming languages. But it seems that there’re several really serious attempts to collect this information .

By looking at the wikibooks: List of hello world programs you can find a lot of HelloWorld programs from more traditional languages such as Pascal or C to something like PostScript or PDP-8 assembler!.

Very interesting!