For this demo I'm going to use the Java3D builder created for previous posts.
The TriangleArray class will be used to create the grid to plot the function . Two triangles will be create for each set of 4 points. For future posts I'm going to try to change this to support TriangleStripArray or QuadArray.
In order to create each coordinate of the plane, a function that maps between the iteration number and the real coordinate to be plotted is required. In order to do this the createMapFunc was created, this function returns a function that maps between two coordinates.
Closure createMapFunc(int x1,int x2,double y1,double y2) {
double m = (y2 - y1)/(x2 - x1);
double b = y1 - m*x1;
return { x -> m*x + b}
}
Closure createFloatMapFunc(int x1,int x2,double y1,double y2) {
Closure f = createMapFunc(x1,x2,y1,y2);
return { (float)f(it)};
}
Given this we can now create the TriangleArray data required to plot the function:
Geometry createGeometry(Closure f,double min,double max,int gridSize) {
Closure fInter = createFloatMapFunc(0,gridSize-1,min,max);
TriangleArray ta = new TriangleArray(((gridSize-1)**2)*6,
TriangleArray.COORDINATES
|TriangleArray.NORMALS
);
int idx = 0;
float x,y,z;
for ( iY in (0..(gridSize-2))) {
for( iX in (0..(gridSize-2))) {
// First triangle
x = fInter(iX);
y = fInter(iY);
z = (float) f(x,y);
ta.setCoordinate(idx,new Point3f(x,y,z));
x = fInter(iX+1);
y = fInter(iY);
z = (float) f(x,y);
ta.setCoordinate(idx+1,new Point3f(x,y,z));
x = fInter(iX);
y = fInter(iY+1);
z = (float) f(x,y);
ta.setCoordinate(idx+2,new Point3f(x,y,z));
idx += 3;
// Second triangle
x = fInter(iX+1);
y = fInter(iY);
z = (float) f(x,y);
ta.setCoordinate(idx,new Point3f(x,y,z));
x = fInter(iX+1);
y = fInter(iY+1);
z = (float) f(x,y);
ta.setCoordinate(idx+1,new Point3f(x,y,z));
x = fInter(iX);
y = fInter(iY+1);
z = (float) f(x,y);
ta.setCoordinate(idx+2,new Point3f(x,y,z));
idx += 3;
}
}
return ta;
}
The function to be plotted is a parameter to the createGeometry function.
For this example the following function will be used:
def f = { x,y -> Math.cos(x+y)*Math.sin(x-y)}
Now that we have the code to generate the 3D function geometry we can create the Java3D/Swing required elements by using the Swing, Java3D and SimpleUniverse builders.
SwingBuilder sb = new SwingBuilder();
SimpleUniverseBuilder sub = new SimpleUniverseBuilder();
Java3dBuilder jb = new Java3dBuilder();
JFrame aFrame = sb.frame(title:"Function",size:[500,500]){
panel(layout: new FlowLayout()) {
thePanel = panel(preferredSize:[500,500],
layout:new BorderLayout())
}
}
SimpleUniverse univ =
sub.simpleUniverse() {
viewingPlatform(nominalViewingTransform:true) {
orbitBehavior(
flags:OrbitBehavior.REVERSE_ALL,
bounds:new BoundingSphere(
new Point3d(0.0,0.0,0.0),
100.0))
}
viewer() {
view(minFrameCycleTime:5)
}
}
thePanel.add(univ.getCanvas(),BorderLayout.CENTER);
BranchGroup bg =
jb.branchGroup() {
transformGroup(
capability:
TransformGroup.ALLOW_TRANSFORM_WRITE) {
shape3d(geometry:createGeometry(f,-2.5,2.5,20),
appearance:polyAppearance())
}
}
bg.compile();
univ.addBranchGraph(bg);
aFrame.show()
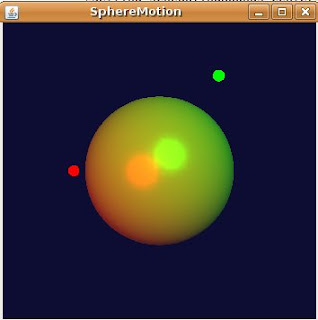
The result of running the program looks like this:

As a last detail, the appearance of the surface is created with the createPolyAppearance function:
Appearance polyAppearance() {
Appearance app = new Appearance();
PolygonAttributes pa = new PolygonAttributes();
pa.setPolygonMode(PolygonAttributes.POLYGON_LINE);
app.setPolygonAttributes(pa);
return app;
}
Code for this experiment can be found here.
In future posts I'm going to try to add more features, like materials applied to the surface geometry, axis lines, etc.