This post presents a little
Flex program exercises features such as graphics, language interaction and style separation.
This is the third of series of posts that explore features across different platforms such as
JavaFX Script or
Silverlight with IronRuby.
Code is this post was created using
Flex SDK 3.1.
The example
As described in the
first post the example is a:
A little program that calculates and plots a polynomial that touches four points selected by the user. The user can move any of the given points in the screen and the polynomial will be recalculated and replotted while moving it.
The
Neville's algorithm is used in order to find the polynomial that touches all the given points.
Developing Flex programs
Working with Flex was a nice experience. Adobe provides a lot of
documentation along with lots blogs and articles from developers using it.
As with JavaFX Script and Silverlight Dynamic Languages SDK the Flex SDK provides command line tools to develop programs. Only a text editor is required to start programming! . For creating this example I used
Emacs with an
actionscript-mode and for MXML the
nxml-mode.
The program
The final program looks like this:
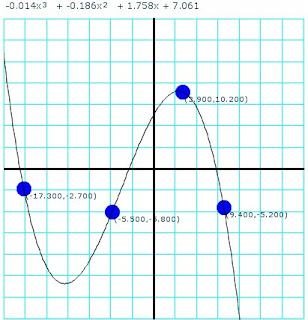
A running version of this program can be found
here.
In the following sections some parts of the program will be presented.
Utility classes
The following utility function was very handy when creating new arrays.
public class Utils
{
public static function createArray(numberOfElements:int,aFunction:Function):Array
{
var result:Array = new Array(numberOfElements);
for(var i:int = 0;i < numberOfElements;i++)
{
result[i] = aFunction(i);
}
return result;
}
}
It creates an array of
numberOfElements elements and initializes each entry with the result of calling a function for each index.
The Polynomial class
This class provides basic functionality for manipulating
polynomials.
public class Polynomial
{
private var coefficients:Array;
public function get coefficientValues():Array
{
return coefficients;
}
public function Polynomial(coefficients:Array)
{
this.coefficients = coefficients;
}
public function evaluate(x:Number):Number
{
var result:Number = 0.0;
for ( var i:int = 0; i < coefficients.length; i++ )
{
result += coefficients[i]*Math.pow(x,i);
}
return result;
}
public function multiplyByTerm(coefficient:Number,exponent:int):Polynomial
{
var originalExponent:int = coefficients.length;
if (coefficient == 0.0)
return new Polynomial(new Array(0));
else
return new Polynomial(
Utils.createArray(originalExponent+exponent ,
function(i:int):Number {
return (i < exponent) ? 0 : coefficients[i-exponent]*coefficient;
}));
}
public function multiply(p:Polynomial):Polynomial
{
var parts:Array = Utils.createArray(coefficients.length,
function(i:int):Polynomial {
return p.multiplyByTerm(coefficients[i],i);
});
var result:Polynomial = new Polynomial(new Array());
for each (var aPart:Polynomial in parts)
{
result = result.add(aPart);
}
return result;
}
public function add(p:Polynomial) : Polynomial
{
var length1:int= coefficients.length;
var length2:int = p.coefficients.length;
var resultArray:Array = null;
if (length1 == length2)
{
resultArray = Utils.createArray(length1,
function(i:int):Number {
return coefficients[i]+p.coefficients[i];
});
}
else
{
if (length1 > length2)
{
resultArray = Utils.createArray(length2,
function(i:int):Number {
return coefficients[i]+p.coefficients[i];
});
for(var i:int = length2;i <= length1 - 1;i++)
{
resultArray.push(coefficients[i]);
}
}
else
{
resultArray = Utils.createArray(length1,
function(i:int):Number {
return coefficients[i]+p.coefficients[i];
});
for(var j:int = length1;j <= length2 - 1;j++)
{
resultArray.push(p.coefficients[j]);
}
}
}
return new Polynomial(resultArray);
}
}
The Algorithm
The implementation of
Neville's algorithm is the following:
public class NevilleCalculator
{
private var theConverter : PlaneToScreenConverter;
...
public function createPolynomial(screenPoints:Array):Polynomial
{
var numberOfPoints:int = screenPoints.length;
var matrix:Array = Utils.createArray(numberOfPoints,
function(i:int):Array {
return Utils.createArray(i+1,
function(i:int):Polynomial
{
return new Polynomial([]);
}
);
});
for(var pindex:int = 0;pindex < numberOfPoints;pindex++)
{
var coefficients:Array = [converter.convertToPlaneY(screenPoints[pindex].y)];
matrix[pindex][0] = new Polynomial(coefficients);
}
var xs:Array = Utils.createArray(numberOfPoints,function(i:int):Number { return converter.convertToPlaneX(screenPoints[i].x); } );
var ys:Array = Utils.createArray(numberOfPoints,function(i:int):Number { return converter.convertToPlaneY(screenPoints[i].y); } );
for(var i:int = 1; i < numberOfPoints;i++) {
for(var j:int = 1;j <= i;j++) {
var q:Number = xs[i] - xs[i-j];
var p1:Polynomial = new Polynomial([ -1.0*xs[i-j]/q, 1.0/q]);
var p2:Polynomial = new Polynomial([ xs[i]/q, -1.0/q ]);
matrix[i][j] = p1.multiply(matrix[i][j-1]).add(p2.multiply(matrix[i-1][j-1]));
}
}
return matrix[numberOfPoints-1][numberOfPoints-1];
}
}
Plane to screen conversion
As with the other examples, a class was used to convert between screen and Cartesian plane coordinates.
public class PlaneToScreenConverter
{
public var screenMaxX : Number;
public var screenMaxY : Number;
public var screenMinX : Number;
public var screenMinY : Number;
public var planeMinX : Number;
public var planeMinY : Number;
public var planeMaxX : Number;
public var planeMaxY : Number;
...
public function convertToScreenX(x:Number):int {
var m:Number = ((screenMaxX - screenMinX)/(planeMaxX - planeMinX));
var b:Number = screenMinX - planeMinX*m ;
return (m*x + b);
}
public function convertToScreenY(y:Number):int {
var m:Number = ((screenMaxY - screenMinY)/(planeMaxY - planeMinY));
var b:Number = screenMinY - planeMinY*m ;
return (m*y + b);
}
public function convertToPlaneX(x:int):Number{
var m:Number = ((planeMaxX - planeMinX)/(screenMaxX - screenMinX));
var b:Number = planeMinX- screenMinX*m ;
return (m*x + b);
}
public function convertToPlaneY(y:int):Number {
var m:Number = ((planeMaxY - planeMinY)/(screenMaxY - screenMinY));
var b:Number = planeMinY - screenMinY *m ;
return (m*y + b);
}
}
Plotting the polynomial
In order to plot the polynomial two classes were created. One that used to create all the points to be plotted(
FunctionPlotter) and the other to represent the graphic elements in the screen(
PlottedFunction).
The
FunctionPlotter class looks like this:
public class FunctionPlotter
{
private var converter : PlaneToScreenConverter;
private var steps:int = 250;
private var initialX:Number = -1.0;
private var finalX:Number = 1.0;
private var poly:Polynomial;
public function FunctionPlotter(aConverter : PlaneToScreenConverter,poly:Polynomial)
{
converter = aConverter;
this.poly = poly;
}
public function createPolyPoints():Array
{
var m:Number = (finalX - initialX)/(steps - 0);
var b:Number = finalX - m*steps;
var increment:Number = Math.abs(converter.planeMaxX - converter.planeMinX) / steps;
var currentX:Number = Math.min(converter.planeMaxX, converter.planeMinX);
var result:Array = new Array(steps);
for (var i:int = 0; i < steps;i++)
{
var currentY:Number = poly.evaluate(currentX);
result[i] = new Point(converter.convertToScreenX(currentX)*1.0,
converter.convertToScreenY(currentY)*1.0);
currentX = currentX + increment;
}
return result;
}
}
The
PlottedFunction class looks like this:
public class PlottedFunction extends UIComponent
{
private var points:Array;
public function PlottedFunction()
{
this.points = new Array();
}
public function get pointsToPlot():Array
{
return points;
}
public function set pointsToPlot(newPoints:Array):void
{
points = newPoints;
invalidateDisplayList();
}
protected override function updateDisplayList(w:Number,h:Number):void
{
graphics.clear();
graphics.lineStyle(1, 1, 1);
if (points.length > 0)
{
graphics.moveTo(points[0].x,points[0].y);
}
for (var i:int = 1; i < points.length;i++) {
graphics.lineTo(points[i].x,points[i].y);
}
}
}
Dragging elements
In order to allow the user to modify the control points a ControlPoint class was created.
[Style(name="pointColor",type="uint",format="Color",inherit="no")]
[Event(name="change", type="flash.events.Event")]
public class ControlPoint extends UIComponent
{
private var theSize:Number = 10;
private var theColor:int = 0x000000;
private var pointLabel:Label;
private var pconverter:PlaneToScreenConverter;
private var numberFormatter:NumberFormatter;
public function ControlPoint()
{
addEventListener(MouseEvent.MOUSE_DOWN,onMouseDown);
addEventListener(MouseEvent.MOUSE_UP,onMouseUp);
pointLabel = new Label();
setPointText();
}
public function get converter() : PlaneToScreenConverter
{
return pconverter;
}
public function set converter(theConverter:PlaneToScreenConverter) : void
{
pconverter = theConverter;
setPointText();
}
public function get formatter() : NumberFormatter
{
return numberFormatter;
}
public function set formatter(numberFormatter:NumberFormatter):void
{
this.numberFormatter = numberFormatter;
setPointText();
}
private function onMouseDown(e:MouseEvent):void
{
startDrag();
addEventListener(MouseEvent.MOUSE_MOVE,onMouseMovingWhileDragging);
}
private function onMouseUp(e:MouseEvent):void
{
removeEventListener(MouseEvent.MOUSE_MOVE,onMouseMovingWhileDragging);
stopDrag();
setPointText();
}
private function onMouseMovingWhileDragging(e:MouseEvent):void
{
dispatchEvent(new Event(Event.CHANGE));
setPointText();
}
public function get size() : Number
{
return theSize;
}
public function set size(value:Number):void
{
theSize = value;
}
override protected function createChildren():void {
super.createChildren();
addChild(pointLabel);
setPointText();
}
private function setPointText() : void
{
this.pointLabel.move(0,0);
if (converter != null && numberFormatter != null) {
var xText:String = numberFormatter.format(converter.convertToPlaneX(x));
var yText:String = numberFormatter.format(converter.convertToPlaneY(y));
pointLabel.text = "("+xText+","+yText+")";
}
}
protected override function updateDisplayList(w:Number,h:Number):void
{
super.updateDisplayList(w,h);
this.pointLabel.move(0,0);
var metrics:TextLineMetrics = pointLabel.getLineMetrics(0);
pointLabel.setActualSize(metrics.width+5,metrics.height+3);
graphics.beginFill(getStyle("pointColor"));
graphics.drawCircle(0,0,size);
graphics.endFill();
}
}
The
Capturing mouse input section of the documentation shows a nice way to allow drag and drop operations on a given object. The only thing that is required is to call the
startDrag method when the mouse button is pressed and call
stopDrag when it is released.
A handler to the MOUSE_MOVE event is added so the coordinates are updated while moving while also raising a CHANGE event which will be useful when trying to update line graph.
One important lesson learned while creating this custom control is that, when having nested controls, the
setActualSize method must be call in the
updateDisplayList method. If not, the nested control will not be presented.
Presenting the polynomial's formula
As with the
Silverlight example, I wasn't able to present superscript characters in in one label control. The Flex label control supports HTML for formatting, however the <sub> and <sup> tag aren't supported.
The solution was to create an horizontal box that holds a sequence of labels with vertical alignment set to
top.
public function createFormulaTextComponents(p:Polynomial,b:Box):void
{
var firstTime:Boolean = true;
b.removeAllChildren();
for(var i:int = 0;i < p.coefficientValues.length;i++)
{
var result:String = "";
var theIndex:Number = p.coefficientValues.length - 1 - i;
if (Math.abs(p.coefficientValues[i]) > 0.001)
{
if (!firstTime)
{
result = result + " + ";
}
if(theIndex != 0)
{
result = result + formatter.format(p.coefficientValues[theIndex]) + "x";
var l:Label = new Label();
l.text = result;
l.styleName = "formula";
b.addChild(l);
if(theIndex != 1)
{
var le:Label = new Label();
le.htmlText = theIndex.toString();
le.styleName = "formulaExponent";
b.addChild(le);
}
}
else
{
result = result + formatter.format(p.coefficientValues[theIndex]);
var cl:Label = new Label();
cl.styleName = "formula";
cl.text = result;
b.addChild(cl);
}
firstTime = false;
}
}
Styling custom controls
Flex supports
CSS styling for controls. Some considerations must be taken when creating properties in custom controls that will be configured using this mechanism.
The
Creating Style Properties article gives a complete explanation on how to create this kind of properties.
Mainly what it requires it's to add an
Style annotation to the control's type annotation. For example in the
ControlPoint class
the color of the point can be configured using the
pointColor style property.
[Style(name="pointColor",type="uint",format="Color",inherit="no")]
[Event(name="change", type="flash.events.Event")]
public class ControlPoint extends UIComponent
{
....
}
Changing this property using a
mx:Style block looks like this:
<mx:Style>
.pointStyle {
pointColor: #0000F5;
}
</mx:Style>
The main program
The main MXML file is presented below. It shows the basic scene with a vertical box that has an horizontal box for the formula's text and a canvas for the function's graph.
The
init is responsible for synchronizing the function's graph with the given control points.
<mx:Application xmlns:langexplr="langexplr.*"
xmlns:mx="http://www.adobe.com/2006/mxml"
initialize="init();"
backgroundColor="0xFFFFFF"
paddingLeft="0" paddingRight="0" paddingTop="0" paddingBottom="0">
<mx:Style>
.alines {
gridLineColor: #00FFFF;
axisLineWidth: 3;
}
.pointStyle {
pointColor: #0000F5;
}
.formula {
paddingLeft: 0;
paddingRight: 0;
textIndent: 0;
fontSize:12;
}
.formulaExponent {
paddingLeft: 0;
paddingRight: 0;
textIndent: 0;
fontSize: 10;
}
</mx:Style>
<mx:Script>
<![CDATA[
import langexplr.*;
import mx.controls.Label;
private var p:Polynomial = null;
private var plotter:FunctionPlotter;
private function init():void
{
var somePoints:Array = [new Point(p1.x,p1.y),
new Point(p2.x,p2.y),
new Point(p3.x,p3.y),
new Point(p4.x,p4.y)];
var poly:Polynomial = nevilleCalculator.createPolynomial(somePoints);
plotter = new FunctionPlotter(converter,poly);
var pointsToPlot:Array = plotter.createPolyPoints();
plotted.pointsToPlot = pointsToPlot;
createFormulaTextComponents(poly,formulaBox);
}
...
}
]]>
</mx:Script>
<mx:NumberFormatter id="formatter" precision="3"/>
<langexplr:PlaneToScreenConverter id="converter"
screenMaxX="400" screenMaxY="0"
screenMinX="0" screenMinY="400"
planeMinX="-20" planeMinY="-20"
planeMaxX="20" planeMaxY="20"/>
<langexplr:NevilleCalculator id="nevilleCalculator" converter="{converter}" />
<mx:Box direction="vertical" width="100%" height="100%">
<mx:Box id="formulaBox" direction="horizontal" verticalAlign="top" horizontalGap="-4" verticalGap="0" paddingLeft="0" paddingRight="0">
</mx:Box>
<mx:Canvas id="c" width="400" height="400" clipContent="true" backgroundColor="0xFFFFFF">
<langexplr:AxisLines converter="{converter}" numberOfSteps="14" styleName="alines"/>
<langexplr:ControlPoint id="p1" x="30" y="120" change="init();" converter="{converter}" formatter="{formatter}" styleName="pointStyle" />
<langexplr:ControlPoint id="p2" x="80" y="100" change="init();" converter="{converter}" formatter="{formatter}" styleName="pointStyle"/>
<langexplr:ControlPoint id="p3" x="190" y="30" change="init();" converter="{converter}" formatter="{formatter}" styleName="pointStyle"/>
<langexplr:ControlPoint id="p4" x="250" y="185" change="init();" converter="{converter}" formatter="{formatter}" styleName="pointStyle"/>
<langexplr:PlottedFunction id="plotted" x="0" y="0" />
</mx:Canvas>
</mx:Box>
</mx:Application>
Deploying the application
Compiling and the application and making it available in a web page is pretty straightforward.
By calling the compiler using the following command:
mxmlc Neville.mxmlA
Neville.swf file is created. This file could be embedded like any other
Flash program.Final words
The experience of developing this little example using Flex was great. The documentation provided by Adobe was very useful.
As with JavaFX script and Silverlight Dynamic Languages SDK it was very nice to be able to create this example using only command line tools and a text editor.
It was interesting to learn a little bit about ActionScript 3. The language has some interesting things. I hope I could learn more about it in the future.
One feature that may be nice to have in AS3 is type inference for local variables. It could be useful to avoid scenarios such as typing
var v:MyClass = new MyClass(); to avoid the
"variable 'v' has no type declaration" warning.
Then creation of basic graphic shapes such as circles or lines was a little more difficult compared to JavaFX or Silverlight, since it cannot be specified directly in the MXML. That is something that seems to be different in
Flex 4 with
FXG.
Code for this post can be found
here.
A running version of this program can be found
here.