APL
APL is an array oriented programming language which means it's good for manipulating vectors, matrices and other kinds of arrays.
APL has many interesting characteristics among them is its syntax which uses non ASCII characters .
Here's a very nice video showing how to implement the Conway's Game Of Life in APL:
A very nice APL resource is the APL Wiki it has lots of information. Another very nice resource is The FinnAPL Idiom Library which contains lots little examples of code. Another nice resource is Vector the journal of the British APL Association which has information on the community around APL related languages.
The examples presented in this post were written using NARS2000 a nice open source implementation of APL.
Polynomial multiplication
As with a previous post on J I'm going to show the implementation of polynomial multiplication .
The following example shows the process of multiplying two polynomials:
(4x3 - 23x2 + x + 1) * (2x2 - x - 3)
= ((4x3 - 23x2 + x + 1) * 2x2) +
((4x3 - 23x2 + x + 1) * -x) +
((4x3 - 23x2 + x + 1) * -3)
= (8x5 - 46x4 + 2x3 + 2x2) +
(-4x4 + 23x3 - x2 - x) +
(-12x3 + 69x2 - 3x - 3)
= (8x5 - 50x4 + 13x3 + 70x2 - 4x - 3)
This example will be used to illustrate the parts of the code in the following sections.
The program
The final program to calculate polynomial multiplication looks like this:
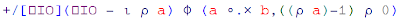
Where
a and b are the polynomials.As with the previous post on J I'm sure there's a shorter way to write this program
(the number of parenthesis seems to indicate this!).
One key aspect to understand APL code is to remember that it evaluates expressions from right to left. See the Order of execution section of the APL Wiki for more information.
A description of each part of this program is presented in the following sections.
Polynomial representation
To represent polynomials we're going to use vectors the following way:
For:
(4x3 + 23x2 + x + 1) the array will be:
1 1 23 4 In APL arrays are written as sequences of numbers separated by spaces (as above). You can manipulate this values easily, for example here we create two variables with two polynomials and add them:

In order to multiply each element of the array by a value we can simply write:

Outer product
The outer product operator lets you apply an operation to all the combinations of the elements of the operands. For example if we want to multiply each value of the two arrays representing the polynomials we want to multiply we can write:

Creating a matrix of intermediate polynomials
We need to obtain a matrix with the intermediate polynomials given the result of the outer product. But first I'm going to introduce the rho function. This function can be used to with one argument (monadic) to obtain the dimensions of the given array for example:

Or it can be used with two arguments (dyadic) to create an array of the given shape.

We can use this function combined with comma function to expand the matrix of polynomials:

The iota function lets you, among other things, create arrays of sequences of values. We're going to use it to create the values used to rotate each polynomial in our matrix:

The rotation of each matrix element is performed using the rotate function as follows:

The final step is to sum every vector in this matrix. We can do that by using the reduce operator (/) . This operator lets you apply a dyad operation to every element of an array accumulating the result. For example:

The nice thing about it is that if you apply it to a matrix, it will do the right thing by summing up every 1d vector. In our case we need to sum the rows so we change the axis of the operation.

Index origin
Before defining the final function we need to take an additional consideration. There is a system variable which modifies the origin of the
iota function among other things. For example:
In other to make our code independent of the value of
IO by using it instead of references to '1' as above.Defining a function
The final function definition looks like this:
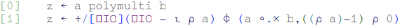
We can use this function as follows:
